Intervalo

Intervalo

Pode-se representar o conjunto dos números reais  associando cada número x ∈ R a um ponto de uma reta r. assim se convencionarmos uma origem O, associando a ela o zero, adotamos uma unidade e um sentido positivo para esta reta, teremos aquela que denominamos reta orientada.

Seja a e b números reais com a < b. os subconjuntos de R a seguir são chamados intervalos.

Intervalo limitado

Intervalo fechado: Números reais maiores ou iguais a a e menores ou iguais a b.

Intervalo: [a, b]
Conjunto: {x ∈ R | a ≤ x ≤ b}
Intervalo aberto: Números reais maiores do que a e menores do que b.

Intervalo: ]a, b[
Conjunto: {x ∈ R | a < x < b}
Intervalo fechado à esquerda: Números reais maiores ou iguais a a e menores do que b.

Intervalo: [a, b[
Conjunto: {x ∈ R | a ≤ x < b}
Intervalo fechado à direita: Números reais maiores do que a e menores ou iguais a b.

Intervalo: ]a, b]
Conjunto: {x ∈ R | a < x ≤ b}

Intervalos ilimitados

Semi reta esquerda, fechada, de origem b: Números reais menores ou iguais a b.

Intervalo: ]-∞ ,b]
Conjunto: {x ∈ R | x ≤ b}
Semi reta esquerda, aberta, de origem b: Números reais menores que b.

Intervalo: ]-∞ ,b[
Conjunto: {x ∈ R | x
Semi reta direita, fechada, de origem a: Números reais maiores ou iguais a a.

Intervalo: [a,+∞ [
Conjunto: {x ∈ R | x ≥ a}
Semi reta direita, aberta, de origem a: Números reais maiores que a.

Intervalo: ]a, +∞ [
Conjunto: {x ∈ R | x>a}
Reta numérica: Números reais.

Intervalo: ] ∞- ,+∞ [
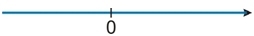
Conjunto: R

Exemplos:

Dados os conjuntos
A= { x ∈ R / -3 < x < 4}
B= {x ∈ R /x ≥ -2}
C= {x ∈ R/0 ≤ x < 4}

Determine por meio de intervalos:
a)A∪ B ∪ C
b)A ∪ C
c)B ∩ C
d)A-C
e)C-B 

Resoluçao:

Vamos lá , primeiramente temos que resolver os conjuntos A , B e C

A = x ∈ ( pertence) a R ( conjunto dos números reais) / ( tal que ) -3 menor que x e menor que 4 , então no caso vai ser todos os números que estiverem entre -3 e 4 , que são eles : { -2,-1,0,1,2 e 3 }

B = fazer o mesmo processo , x maior ou igual a -2 , então vai ser todos os números maiores que -2 , incluindo -2 , que são : { -2,-1,0,1,2,3,4 ...} e assim vai .

C = 0 é menor ou igual a X que é menor que 4 , então ficará : { 0,1,2 e 3 }


Agora determinar por intervalos

a)A∪ B ∪ C = A unido a B unido a C , voce irá somar todos os 3, do menor número de qualquer que seja o conjunto , ao maior , que no caso é o infinito , que ficará da seguinte forma :

Resposta letra a) { -2,-1,0,1,2,3,4 ... } e assim vai , pois o temos um conjunto com terminação indeterminada .

b)A ∪ C = A unido a C , vai unir o conjunto A com o conjunto C , como todos os números contidos no conjunto C já temos no conjunto A , apenas conservamos o conjunto A :

Resposta letra b) {-2,-1,0,1,2,3 }

c)B ∩ C = B interseção a C , vamos separar o que tem em B que também tem em C , ficará :

Resposta letra c) {0,1,2,3}

d)A-C = A-C , no caso , o que tem em A e não tem em C , ficará :

Resposta letra d) {-2,-1}

e)C-B = C-B , o que tem em C que não tem em B , ficará :

Resposta letra e) Tudo o que tem em C , tem em B , então a resposta é conjunto vazio

Resposta : CONJUNTO VAZIO .